Opere matematiche di Luigi Cremona/Intorno ad un'operetta di Giovanni Ceva matematico milanese del secolo XVII

by Luigi Cremona

Intorno ad un’operetta di Giovanni Ceva matematico milanese del secolo XVII

../Considerazioni di storia della geometria in occasione di un libro di geometria elementare publicato a Firenze ../Sur quelques propriétés des lignes gauches de troisième ordre et classe IncludiIntestazione 15 settembre 2020 75% Da definire

Questo testo è completo.

Luigi Cremona - Opere matematiche (1914)

Intorno ad un’operetta di Giovanni Ceva matematico milanese del secolo XVII

◄

Considerazioni di storia della geometria in occasione di un libro di geometria elementare publicato a Firenze

Sur quelques propriétés des lignes gauches de troisième ordre et classe

►

23.

INTORNO AD UN’OPERETTA DI GIOVANNI CEVA

MATEMATICO MILANESE DEL SECOLO XVII.

---

Rivista ginnasiale e delle Scuole tecniche e reali, t. VI (1859), pp. 191-206.

---

Intendo parlare di un breve opuscolo, stampato in Milano nel 1678 ed avente per titolo: De lineis rectis se invicem secantibus statica constructio. Ne è autore Giovanni Ceva, milanese, una nostra gloria dimenticata o poco nota fra noi, malgrado che un illustre geometra straniero, il signor Chasles, ne abbia fatto onorevole menzione nella sua celebre opera: Aperçu historique sur l’origine et le développement des méthodes en géométrie.

L’opuscolo di cui si tratta è dedicato a Ferdinando Carlo duca di Mantova.

Nel proemio narra l’autore com’egli adolescente cercasse negli studî un conforto a’ suoi infortunî. Dedicatosi alla geometria, quae et rerum varietate et genere ipso caeteris (scientiis) anteire visa est, innamorato delle somme opere di Apollonio, Archimede, Pappo e degli altri grandi antichi, sciolse le vele ai venti sperando che alcun caso felice gli facesse trovare nuovi lidi e inesplorate regioni. Come tutti i geometri di quel tempo, incominciò suoi tentativi vaneggiando dietro la quadratura del cerchio. Quante illusioni, quanti disinganni in quelle inutili ricerche! Ter mihi conciliata recti et curvi dissidia insomnes noctes persuasere, ter normam fugit figura contumax et tenax sui. Tamen, ut frustratis semel iterumque laboribus lux aliqua spesque nova subinde oriebatur, tandiu relabenti saxo Sisyphus pervicax inhaesi, donec adhibita, novissime irrito successu indivisibilia Cavallerii omnem animi pertinaciam domuere. Visto adunque riuscir vano ogni sforzo; cadutagli anco l’estrema speranza riposta in quel potente stromento di ricerche, che è grande gloria del nostro Cavalieri; mancando oltracciò a quel tempo il mezzo di convincersi a priori della vanità di quei tentativi, il Ceva stimò che non senza alto consiglio fosse posto tal freno alle menti umane, e accettò come dono di Dio e conforto alle patite delusioni quelle novità in cui ebbe a scontrarsi, e che formano il soggetto del libro. Imperocchè (com’ei continua a narrare) messi da parte gli ordinari apparati dell’antica geometria, giovandosi invece di considerazioni desunte dalla meccanica, gli avvenne di scoprire cose certamente nuove per quel tempo. La novità e l’efficacia del metodo da lui trovato lo persuasero a farlo di pubblica ragione, lusingandosi che altri avesse a perfezionare ed ampliare l’opera sua. Vana speranza, poichè pare che il suo libro passasse immeritamente inosservato o cadesse presto nell’obblio.

La ingenua modestia di quel giovane, certamente nato e cresciuto a nobilissimi sensi, risplende soprattutto nella conclusione del proemio. Non desiderio di fama, ei dice, lo spinse a pubblicare questo libro, poichè qual fama sperare in tanta abbondanza e celebrità di autori? Solo confida e fa voti che il suo lavoro riesca di alcuna utilità e compendiosità nelle ricerche geometriche. Chiede perdono al lettore, s’ei troverà parecchie cose quibus desit suprema manus, e se ne scusa con ciò che dallo studio troppo lo distrassero altre cure ed anche amicorum et familiarium querimoniae male in his collocatum iuventutis florem existimantium. Che se pur qualche cosa parrà non del tutto spregevole, l’autore invita ad averne intera gratitudine al suo maestro Donato Rossetti, cuius primis institutionibus, si quid in me est bonarum artium, debeo.

I pregi di questo opuscolo sono molti e lo rendono degnissimo d’essere meglio conosciuto. Mirabile la semplicità e l’eleganza del metodo statico col quale l’autore svolge la maggior parte del suo lavoro. Soprattutto reca sorpresa il trovare qui alcuni elegantissimi teoremi che si direbbero appartenere alla moderna geometria segmentaria, e che infatti vennero generalmente attribuiti a geometri posteriori al Ceva.

L’opuscolo consta di due parti, la prima delle quali soltanto corrisponde al titolo del libro. Essa si divide in due libri, ciascuno distinto in proposizioni. Il primo libro incomincia con certi assiomi e lemmi che sono propri della statica ed invero si riferiscono ai centri di gravità de’ sistemi discreti. Poi seguono cinque proposizioni fondamentali, che l’autore denomina elementi. Il secondo elemento può enunciarsi così:

Dai vertici A, B, C di un triangolo qualsivoglia ABC (fig. 1.ª) si conducano tre rette concorrenti in uno stesso punto O e incontranti rispettivamente i lati opposti ne’ punti A’, B’, C’; inoltre ai vertici A, B, C si suppongano applicati tre pesi (o tre forze parallele in direzione arbitraria) di grandezze proporzionali ad a, b, c, per modo che si abbia:

1)	a : b = BC’ : AC’     a : c = CB’ : AB’

allora ne seguirà:

2)	b : c = CA’ : BA’

ed inoltre:

3)	b + c : a = AO : A’O c + a : b = BO : B’O a + b : c = CO : C’O.

Dimostrazione. In causa delle (1) il centro di gravità comune de’ pesi applicati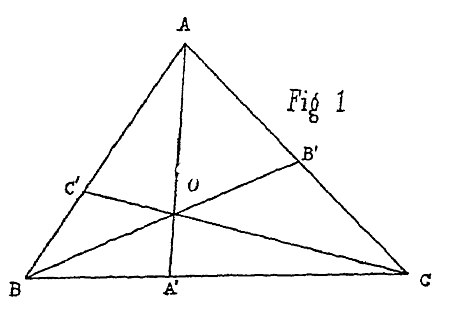Fig 1 in A e B è C’, ed il centro dei pesi applicati in A e C è B’. Dunque il centro de’ tre pesi a, b, c dovrà cadere sì sulla C’C che sulla B’B, cioè sarà il punto O comune a queste due rette. Per conseguenza il centro de’ pesi b, c dovrà essere nella AO, ossia cadrà in A’. Dall’essere il centro de’ due pesi b + c ed a applicati l’uno in A’ e l’altro in A segue la prima delle relazioni (3). Analogamente si dica delle altre due.

Se l’enunciato del precedente teorema si ristringe alla figura che risulta togliendo dalla 1.ª le rette AA’ e BC si ha l’elemento primo. Il quinto elemento può enunciarsi così:

Sui lati di un quadrigono qualsivoglia (piano o gobbo, convesso o concavo) ABCD (fig. 2.ª e 3.ª) si fissino quattro punti E, F, G, H in modo che fra i segmenti risultanti sussista la relazione seguente:

4)	AE . BF . CG . DH = BE . CF . DG . AH

le rette EG, FH giaceranno sempre in uno stesso piano e si segheranno in un punto I. Se inoltre ai vertici del quadrigono si applichino quattro pesi a, b, c, d in modo che si abbia:

5)	a : b = BE : AE,     b : c = CF : BF,     c : d = DG : CG

allora sarà inoltre:

6)	d : a = AH : DH

e:

7)	a + d : b + c = FI : HI,     a + b : c + d = GI : EI.

Dimostrazione. Si moltiplichino fra loro, termine a termine, le proporzioni (5); risulterà:

a : d = BE . CF . DG : AE . BF . CG.

Ma la relazione (4) può scriversi anche così:

BE . CF . DG : AE . BF . CG = DH : AH

dunque si avrà:

a : d = DH : AH

il che dimostra la sussistenza della (6). Le relazioni (5) e (6) esprimono che E è il centro di gravita de’ pesi a, b, F è il centro de’ pesi b, c, G è il centro de’ pesi c, d, ed H è il centro de’ pesi d, a. Dunque il centro de’ quattro pesi a, b, c, d dovrà trovarsi tanto nella EG che nella FH; ossia queste due rette devono giacere in uno stessoFig 2 Fig 3 piano e segarsi nel punto I centro de’ quattro pesi suddetti. Dall’essere I il centro de’ due pesi a + d, b + c applicati in H, F, ed anche il centro de’ due pesi a + b, c + d applicati in E, G seguono evidentemente le relazioni (7). A ciò che precede possiamo aggiungere quanto segue. Sulle rette AC, BD diagonali del quadrigono prendansi due punti K, L per modo che sia:

a : c = CK : AK,     b : d = DL : BL

la retta KL passerà anch’essa pel punto I e si avrà:

a + c : b + d = LI : KI.

Moltiplicando fra loro, termine a termine, le proporzioni:

a : c = CK : AK,     c : d = DG : CG,     d : b = BL : DL,     b : a = AE : BE

si ottiene l’eguaglianza:

CK . DG . BL. AE = AK . CG . DL . BE;

così pure dalle proporzioni:

a : c = CK : AK,     c : b = BF : CF,     b : d = DL : BL,     d : a = AH : DH

si ha la:

CK . BF . DL . AH = AK . CF . BL . DH.

Il che prova che la proprietà espressa dal teorema superiore (elemento quinto) sussiste simultaneamente pei tre quadrigoni ABCD, ACDB, ACBD aventi i vertici ne’ medesimi quattro punti A, B, C, D.

Se nella fig. 2.ª si riuniscono in un solo i punti B, F, C si ha l’elemento terzo.

Se nella fig. 3.ª si suppone che il punto I cada nell’intersezione dei lati AB, CD si ha l’elemento quarto.

Nelle numerose proposizioni che tengono dietro si espongono svariate proprietà che sono tutti corollari de’ citati elementi. Parecchie di tali proposizioni sono problemi ne’ quali, supposti conosciuti alcuni de’ rapporti fra i segmenti rettilinei che entrano nella figura di un elemento, si cercano tutti gli altri.

Nel secondo elemento, se si moltiplicano fra loro, termine a termine, le proporzioni:

b : c = CA’ : BA’,     c : a = AB’ : CB’,     a : b = BC’ : AC’

si ha l’eguaglianza:

8)	CA’ . AB’ . BC’ = BA’ . CB’ . AC’

ossia;

Se dai vertici di un triangolo si conducono tre rette passanti per uno stesso punto, esse determinano sui lati opposti sei segmenti tali, che il prodotto di tre non aventi termini comuni è eguale al prodotto degli altri tre.

Questo bel teorema, ora ben noto come uno de’ principali nella teorica delle trasversali, è interamente dovuto al nostro Ceva. Prima che il signor Chasles gliene rivendicasse il merito, lo si attribuiva a Giovanni Bernoulli. Noi lo chiameremo il teorema di Ceva.

Dalle (3) si ricava:

a + b + c : a = AA’ : A’O
a + b + c : b = BB’ : B’O
a + b + c : c = CC’ : C’O

da cui:

9)	${\frac {\mathrm {A'O} }{\mathrm {AA'} }}+{\frac {\mathrm {B'O} }{\mathrm {BB'} }}+{\frac {\mathrm {C'O} }{\mathrm {CC'} }}=1.$

Così dalle medesime (3) si deduce:

a + b + c : b + c = AA’ : AO
a + b + c : c + a = BB’ : BO
a + b + c : a + b = CC’ : CO

e però:

10)	${\frac {\mathrm {AO} }{\mathrm {AA'} }}+{\frac {\mathrm {BO} }{\mathrm {BB'} }}+{\frac {\mathrm {CO} }{\mathrm {CC'} }}=2.$

Le equazioni (9) e (10) esprimono altrettanti teoremi, ossia sono altrettante forme del teorema di Ceva:

Dai vertici di un triangolo si tirino tre rette passanti per uno stesso punto e terminate ai lati opposti. Ciascuna di queste tre rette è divisa dal punto comune in due segmenti, l’uno adiacente a un vertice, l’altro adiacente al lato opposto. La somma de’ rapporti de’ primi segmenti alle intere rette è eguale a 2. La somma de’ rapporti degli altri segmenti alle intere rette è eguale all’unità.

Continuando ad occuparci della figura 1.ª osserviamo che i triangoli BA’O, AB’O hanno un angolo eguale, e però per un noto teorema (Geometria del Legendre, lib. III, prop. 24) si avrà:

BA’O : AB’O = BO . A’O : AO . B’O

analogamente:

CB’O : BC’O = CO . B’O: BO . C’O
AC’O : CA’O = AO . C’O : CO . A’O.

Queste proporzioni moltiplicate fra loro danno:

BA’O . CB’O . AC’O = AB’O . BC’O . CA’O

ossia:

Se dai vertici di un triangolo si tirano tre rette passanti per uno stesso punto, esse danno luogo a sei nuovi triangoli tali, che il prodotto delle aree di tre non consecutivi è eguale al prodotto delle aree degli altri tre.

Se nella fig. 1.ª si tira la retta B’C’ i triangoli ABC, AB’C’ avendo un angolo comune, danno:

ABC : AB’C’ = AB . AC : AB’. AC’.

Ora dalle (1) si ha:

AB : AC’ = a + b : b
AC : AB’ = a + c : c

quindi:

AB . AC : AB’ . AC’ = (a + b)(a + c): bc

e per conseguenza:

11)	ABC : AB’C’ = (a + b)(a + c): bc.

I triangoli OBC, OB’C’, avendo un angolo eguale, danno analogamente:

OBC : OB’C’ = OB . OC : OB’ . OC’;

ma moltiplicando fra loro la seconda e la terza delle (3) si ha:

OB . OC : OB’. OC’ = (a + b)(a + c) : bc

quindi:

12)	OBC : OB’C’ = (a + b)(a + c) : bc.

Dal confronto delle (11) e (12) concludiamo pertanto:

ABC : AB’C’ = OBC : OB’C’

formola esprimente un teorema. Analogamente si trova:

ABC : A’BC’ = OCA : OC’A’
ABC : A’B’C = OAB : OA’B’

le quali danno facilmente le due seguenti eguaglianze:

AB’C’ . OBC + BC’A’ . OCA + CA’B’. OAB = ABC . A’B’C’
${\frac {\mathrm {OB'C'} }{\mathrm {AB'C'} }}+{\frac {\mathrm {OC'A'} }{\mathrm {BC'A'} }}+{\frac {\mathrm {OA'B'} }{\mathrm {CA'B'} }}=1,$

esprimenti due eleganti teoremi.

Dal suo primo elemento il Ceva deduce un teorema che certamente egli ignorava essere antico. Dalle (1), (2) e (3) si hanno le proporzioni:

AC’ : BC’ = b : a,     BO : B’O = c + a : b,     B’C : AC = a : c + a

le quali moltiplicate fra loro somministrano:

AC’ . BO . B’C = BC’ . B’O . AC.

Questa formola applicata al triangolo ABB’ segato dalla trasversale CC’ dà il teorema:

Una trasversale qualunque determina sui lati di un triangolo sei segmenti tali che il prodotto di tre non aventi termini comuni è eguale al prodotto degli altri tre.

È questo un teorema notissimo e fondamentale nella geometria segmentaria. L’opera più antica in cui lo si trovi è il trattato di geometria sferica di Menelao (80 anni dopo C.); volgarmente però lo attribuiscono a Tolomeo (vissuto nel secolo successivo), forse perchè l’Almagesto è opera meglio letta di quella di Menelao.

Il teorema medesimo si estende, com’è noto, ad un poligono qualsivoglia (Carnot, Essai sur la théorie des transversales).

L’autore applica il suo metodo anche alla dimostrazione di proprietà conosciute. Ai vertici di un triangolo ABC (fig. 1.ª) si suppongano applicati tre pesi, tali che si abbia:

a : b : c = BC : CA : AB.

Sia A’ il centro di gravità dei pesi b, c applicati in B, C; avremo

BA’ : CA’ = c : b = AB : AC,

dunque, per un noto teorema (Legendre, lib. III, prop. 17), la retta AA’ sarà la bisettrice dell’angolo A. Analogamente le rette BB’, CC’ saranno le bissettrici degli angoli B, C. Dunque, in virtù del secondo elemento, arriviamo al noto teorema:

Le bisettrici degli angoli interni di un triangolo qualunque concorrono in uno stesso punto.

Ai vertici di un triangolo ABC (fig. 4.ª) si suppongano applicate tre forze paralleleFig 4 a, b, c, la prima delle quali sia in senso contrario alle altre due, ed inoltre si abbia:

a : b : c = BC : CA: AB.

Allora il punto A’ cadrà fra B e C, ma B’, C’ cadranno ne’ prolungamenti de’ lati CA, AB; AA’ sarà la bissettrice dell’angolo interno A, mentre BB’ e CC’ saranno le bissettrici degli angoli esterni supplementi degli interni B e C. Avremo quindi:

In un triangolo le bissettrici de’ supplementi di due angoli e la bissettrice del terzo angolo concorrono in uno stesso punto.

Se i pesi applicati ai vertici del triangolo ABC (fig. 1.ª) sono eguali, A’, B’, C’ sono i punti medi de’ lati, epperò:

Le tre mediane di un triangolo concorrono in uno stesso punto.

Ai vertici del triangolo ABC siano applicate tre forze parallele a, b, c tali che si abbia:

$a:b:c={\frac {\mathrm {BC} }{\cos \mathrm {A} }}:{\frac {\mathrm {CA} }{\cos \mathrm {B} }}:{\frac {\mathrm {AB} }{\cos \mathrm {C} }}$

avremo quindi:

BA’ : CA’ = c : b = AB . cos B : AC . cos C.

Ma AB . cosB e AC . cos C sono i valori de’ segmenti in cui il lato BC è diviso dalla perpendicolare condotta su di esso dal vertice A; dunque AA’ è perpendicolare a BC. Così BB’ e CC’ sono perpendicolari rispettivamente a CA ed AB. Concludiamo pertanto che:

Le tre altezze di un triangolo passano per uno stesso punto.

Dallo stesso secondo elemento l’autore ricava anche teoremi della geometria a tre dimensioni. Basti addurre il seguente esempio (lib. I, prop. 23):

Sia OABC un tetraedro (fig. 5.ª); sugli spigoli OA, OB, OC siano presi ad arbitrio i punti a’, b’, c’; si tirino le rette Bc’, Cb’ concorrenti in a; Ca’, Ac’ concorrenti in b;Fig 5 Ab’, Ba’, concorrenti in c; indi si tirino le Oa, Ob, Oc, che incontrino BC, CA, AB rispettivamente in A’, B’, C’.

Si dichiara che le rette AA’, BB’, CC’ passano per uno stesso punto o, e che le Aa, Bb, Cc, Oo, A’a’, B’b’, C’c’, passano pure per uno stesso punto F.

Dimostrazione. Ai vertici A, B, C, O del tetraedro s’intendano applicati quattro pesi α, β, γ, δ in modo che sia:

α : δ = Oa’ : Aa’,     β : δ = Ob’ : Bb’,     γ : δ = Oc’ : Cc’,

allora, per l’elemento secondo, A’ sarà il centro de’ pesi β, γ, B’ il centro de’ pesi γ, α, e C’ quello de’ pesi α, β: dunque le rette AA’, BB’, CC’ concorreranno nel centro o de’ pesi α, β, γ. Essendo del pari a, b, c i centri delle tre terne di pesi βγδ, γαδ, αβδ, ne segue che le rette Aa, Bb, Cc, Oo devono incrociarsi nel centro F de’ quattro pesi α, β, γ, δ. D’altra parte a’ è il centro de’ pesi α, δ ed A’ quello de’ pesi β, γ; dunque la retta A’a’ dovrà anch’essa passare per F. Lo stesso vale per le rette B’b’, C’c’.

Se i quattro pesi α, β, γ, δ sono eguali, il teorema precedente somministra le notissime proprietà:

Le rette che congiungono i punti medi degli spigoli opposti di un tetraedro passano per uno stesso punto. I sei piani che passano rispettivamente per i sei spigoli e dimezzano gli spigoli opposti passano per uno stesso punto.

Da ultimo riporterò un elegante teorema che il signor Chasles ha osservato essere una diversa espressione del teorema di Ceva. Avendosi (fig. 1.ª):

${\frac {\mathrm {AO} }{\mathrm {A'O} }}={\frac {b+c}{a}},$     ${\frac {\mathrm {AC'} }{\mathrm {BC'} }}={\frac {b}{a}},$     ${\frac {\mathrm {AB'} }{\mathrm {CB'} }}={\frac {c}{a}}$

ne segue:

${\frac {\mathrm {AO} }{\mathrm {A'O} }}={\frac {\mathrm {AC'} }{\mathrm {BC'} }}+{\frac {\mathrm {AB'} }{\mathrm {CB'} }}.$

Ora la fig. 1.ª rappresenta un quadrigono AB’OC’ di cui AO è una diagonale e BC è la retta che congiunge i punti di concorso de’ lati opposti. Dunque:

In ogni quadrigono la diagonale che parte da un vertice divisa pel suo prolungamento sino alla retta che congiunge i punti di concorso de’ lati opposti è eguale alla somma de’ lati uscenti dallo stesso vertice divisi rispettivamente pe’ loro prolungamenti sino ai lati opposti.

Importanti conseguenze l’autore ricava anche dagli altri tre elementi. A cagion d’esempio dal quinto elemento emerge il teorema seguente (fig. 6.ª):

Sia ABCDE una piramide a base quadrangolare, il cui vertice sia il punto E. Sugli spigoli AE, BE, CE, DE si fissino ad arbitrio i quattro punti a’’, b’’, c’’, d’’; si tirino leFig 6 Ab’’, Ba’’ segantisi in a; Bc’’, Cb’’ segantisi in b; Cd’’, DC’’ segantisi in c; Da’’, Ad’’ segantisi in d; indi si tirino le Ea, Eb, Ec, Ed che incontrino rispettivamente gli spigoli AB, BC, CD, DA in a’, b’, c’, d’; le a’c’, b’d’ si seghino in O. Allora i punti a’, b’, c’, d’ divideranno i lati del quadrigono ABCD in otto segmenti tali, che il prodotto di quattro non aventi termini comuni sia eguale al prodotto degli altri quattro. Ed inoltre le rette EO, ac’, bd’, ca’, db’ si incroceranno in uno stesso punto.

Dallo stesso quinto elemento risulta (lib. II, prop. 4):

Se in un quadrigono gobbo si conducano due rette ciascuna delle quali divida due lati opposti in parti proporzionali, queste due rette giaceranno necessariamente nello stesso piano.

Mediante il terzo elemento si dimostra facilmente il teorema che segue (lib. II, prop. 5):

Dai vertici di un triangolo ABC (fig. 7.ª) si tirino tre rette intersecantisi in uno stesso punto; esse incontrino i lati BC, CA, AB ne’ punti A’, B’, C’. Dai vertici del triangolo Fig 7 risultante A’B’C’ si tirino tre nuove rette passanti per uno stesso punto e incontranti i lati B’C’, C’A’, A’B’ ne’ punti A’’, B’’, C’’. Le rette AA’’, BB’’, CC’’ concorreranno in uno stesso punto.

Nel secondo libro s’incontrano proposizioni involgenti non solo rette, ma anche linee curve, e propriamente sezioni coniche. Avanti tutto vi è dimostrato come lemma (indipendentemente dal sovraesposto metodo statico) il bel teorema:

Se un poligono è circoscritto ad una sezione conica, i punti di contatto dividono i lati in segmenti tali che il prodotto di quelli non aventi termini comuni è eguale al prodotto de’ rimanenti.

Attualmente questo teorema è caso particolare di una proposizione assai generale dovuta al celebre Carnot (Géométrie de position).

Il medesimo teorema, combinato col secondo elemento somministra il seguente:

Quando un triangolo è circoscritto ad una sezione conica, le rette che congiungono i vertici ai punti di contatto de’ lati rispettivamente opposti concorrono in uno stesso punto.

Fin qui abbiamo riprodotti i teoremi dimostrati dal Ceva, oltre a quei corollari i quali, sebbene non esplicitamente da lui dichiarati, pure gli ponno essere ragionevolmente attribuiti, perchè in modo immediato emanano dalle cose sue. Non facciamo parola della seconda parte del libro (Appendix Geometrica), perchè contiene materie affatto diverse e trattate con metodi non aventi alcuna relazione col metodo statico sopra menzionato. Di quest’appendice non è fatta alcuna menzione nel frontispizio dell’opera, benchè, come avverte anche il signor Chasles, ne sia meritevolissima. Dell’aver riunito in un solo opuscolo cose sì disparate come la Statica constructio e l’Appendix Geometrica l’autore si giustifica così: Visum est appendicis loco adjicere his problematibus theoremata quaedam, partim antiquis geometriae legibus, partim Cavalleriana methodo a me soluta, quamvis ex superius dictis minime pendeant. Cum enim in circulo inutiliter quadrando, haec omnia non inutiliter sint inventa, par erat, ut in eodem volumine luce publica fruerentur, quamvis opportunius suis in tenebris latuissent.

Ora ci corre obbligo di menzionare un geometra francese, Coriolis, che ha molto illustrato il metodo statico, di cui è qui discorso. Egli, senza conoscere l’opera del nostro Ceva, giunse da sè alla medesima invenzione, e fino dal 1811 indicò in una sua memoria come, col soccorso di considerazioni statiche, si possono dimostrare i due modi di generazione dell’iperboloide ad una falda. Poi dalle medesime considerazioni dedusse parecchi teoremi di geometria, pubblicati nel 1819 nel periodico: Annales de Mathématiques dell’illustre Gergonne. Da ultimo riassunse quelle ricerche in una breve memoria (Sur la théorie des momens considérée comme analyse des rencontres des lignes droites) inserita nel cahier 24 del Journal de l’École Polytechnique (anno 1835). A piè della prima pagina di questa memoria l’autore pose questa nota: “M. Olivier vient de me montrer un traité publié en 1678 par Jean Ceva, sous le titre: De rectis se invicem secantibus statica constructio. On voit par le titre même que cet ouvrage contient l’idée de ce petit mémoire, etc.„.

In questa memoria del Coriolis trovansi nove eleganti teoremi, de’ quali qui terremo parola. Alcuni di essi non si trovano nell’opera del Ceva; gli altri sono assai più generali di quelli del Ceva medesimo.

Ecco in che consiste il primo teorema. Abbiasi nello spazio una serie di n punti che si rappresentino ordinatamente coi numeri (1), (2), (3), ... (n). Ciascuno di questi punti, meno l’ultimo, si unisca al successivo in modo da formare una linea spezzata che cominci in (1) e termini in (n). Su ciascun lato della spezzata o sul suo prolungamento si prenda un punto ad arbitrio, il quale si rappresenti coi due numeri che rappresentano i termini del lato corrispondente; per es., il punto preso sulla retta (1)(2) s’indicherà con (12), ecc. Così avremo una seconda serie di punti (12), (23), (34), ... Questi punti congiungansi ai punti della prima serie mediante rette; fra le quali quelle che uniscono punti i cui indici riuniti contengono gli stessi numeri s’incontreranno. Per es., le rette (12)(3) e (1)(23) s’incontreranno in un punto che denoteremo con (123); così s’indicherà con (345) il punto d’intersezione delle rette (34)(5) e (3)(45). In questo modo abbiamo la terza serie di punti: (123) (345), ... Questi punti si uniscano a quelli delle due serie precedenti; fra le rette congiungenti, quelle che collegano punti i cui indici messi insieme comprendono i medesimi numeri, s’incontreranno in uno stesso punto, che si denoterà coll’aggregato di questi stessi numeri. Continuando in questo modo, avverrà sempre che s’incrocino in uno stesso punto tutte quelle rette ai cui termini appartengono indici che riuniti formino uno stesso aggregato di numeri. Il numero delle rette che s’intersecano in uno stesso punto è eguale a quello de’ numeri ivi riuniti, meno uno. Per es., vi saranno r — 1 rette congiungenti punti i cui indici riuniti conterranno le cifre 1, 2, 3, ... r; queste rette passeranno tutte per uno stesso punto, che verrà rappresentato col simbolo (123...r).

Questo teorema si dimostra facilissimamente imaginando applicate ai vertici della spezzata altrettante forze parallele, le grandezze delle quali abbiano fra loro tali rapporti, che il punto della seconda serie preso su un lato qualunque sia il centro delle due forze applicate ai termini di questo lato.

Secondo teorema. Si uniscano i termini della spezzata, onde risulterà un poligono gobbo di n lati. Unito il punto (12...n) col punto (23...n — 1), la congiungente incontrerà il lato (1)(n) del poligono in un punto (1n). Allora ciascun lato del poligono sarà diviso in due segmenti; il prodotto di quelli fra questi segmenti che non hanno termini comuni sarà eguale al prodotto de’ rimanenti.

Questi due teoremi, de’ quali il secondo è la generalizzazione del secondo elemento di Ceva, sono acconci a rappresentare nella sua vera essenza il metodo statico di lui.

Terzo teorema (di Carnot). Un piano qualunque determina sui lati di un poligono gobbo tali segmenti, che formando i due prodotti de’ segmenti non adiacenti, questi prodotti sono eguali.

Questo teorema, del quale è caso particolarissimo quello di Menelao, è una facile conseguenza de’ due che precedono.

Quarto teorema. Fissando quanti punti si vogliano sulla superficie di una sfera, e congiungendoli fra loro con archi di cerchi massimi, si avrà sulle intersezioni di questi archi un teorema affatto analogo al primo. Basterà che nell’enunciato di questo sostituiscansi alle rette gli archi di cerchi massimi.

Il teorema si dimostra imaginando delle forze applicate al centro della sfera e passanti rispettivamente pe’ punti fissati sulla superficie di questa; indi ragionando sulla composizione di queste forze come si fa nel primo teorema per le forze parallele.

Quinto teorema. Il secondo teorema ha il suo analogo sulla sfera, purchè ai segmenti rettilinei sostituiscansi i seni degli archi di cerchi massimi.

Il sesto teorema è un’immediata conseguenza del quinto elemento di Ceva.

Eccone l’enunciato. I lati di un quadrigono gobbo ABCD (fig. 8.ª) si seghino con un piano qualunque ne’ punti P, M, Q, N. Si tiri una trasversale qualunque M’N’ che incontri le rette AD, BC, PQ; poi si tiri un’altra trasversale qualunque PQ le rette AB, CD, MN. Allora le due trasversali M’N’, PQ s’incontreranno.

Se imaginiamo le infinite trasversali, analoghe ad M’N’, tutte appoggiate alle tre rette AD, BC, PQ, esse saranno le generatrici di quella superficie gobba che denominasiFig 8 iperboloide ad una falda. In virtù del precedente teorema, le infinite trasversali, analoghe a PQ, tutte appoggiate alle tre rette AB, CD, MN saranno pure generatrici della medesima superficie. Cioè questa superficie ammette due sistemi di rette generatrici: ogni generatrice dell’un sistema incontra tutte quelle dell’altro, mentre due generatrici del medesimo sistema non sono mai nello stesso piano.

Settimo teorema (di Carnot). Se un punto preso entro un poligono piano di un numero dispari di lati si congiunga a ciascun vertice, e la congiungente si prolunghi sino a determinare due segmenti sul lato rispettivamente opposto, i due prodotti formati coi segmenti non adiacenti sono eguali.

Ecco la dimostrazione di questa proprietà, che è la generalizzazione del teorema di Ceva.

Abbiasi, a cagion d’esempio, il pentagono 1 2 3 4 5; imaginiamo delle forze, P₁, P₂, P₃, P₄, P₅, in equilibrio, applicate al punto interno O e dirette rispettivamente verso i vertici 1, 2, 3, 4, 5. Decomponiamo ciascuna di queste forze in due componenti parallele applicate ai termini del lato rispettivamente opposto. Indichiamo con C₁₃, C₁₄, le componenti della forza P₁, con C₂₄, C₂₅ le componenti della forza P₂, ecc.; con S₁₃, S₁₄ i segmenti determinati sul lato 34 dalla direzione della forza P₁; con S₂₄, S₂₅ i segmenti determinati dalla direzione della forza P₂ sul lato 45, ecc.; con α₁₂ ovvero α₂₁ l’angolo compreso dalle direzioni delle forze P₁, P₂, ecc. Allora, per le note leggi della decomposizione delle forze parallele, avremo le seguenti cinque equazioni:

C₄₁ S₄₁ = C₄₂ S₄₂
C₅₂ S₅₂ = C₅₃ S₅₃
C₁₃ S₁₃ = C₁₄ S₁₄
C₂₄ S₂₄ = C₂₅ S₂₅
C₃₅ S₃₅ = C₃₁ S₃₁.

In questo modo a ciascun vertice sono applicate due forze componenti. Noi potremo disporre delle grandezze delle due forze applicate ad ognuno de’ vertici 1, 2, 3, 4 in modo che la loro risultante passi per O. Allora, per l’equilibrio, sarà necessario che anche le componenti applicate al vertice 5 abbiano una risultante passante per O. Quindi, per le conosciute formole sulla decomposizione delle forze concorrenti, avremo le equazioni:

C₃₁ sen α₃₁ = C₄₁ sen α₄₁
C₄₂ sen α₄₂ = C₅₂ sen α₅₂
C₅₃ sen α₅₃ = C₁₃ sen α₁₃
C₁₄ sen α₁₄ = C₂₄ sen α₂₄
C₂₅ sen α₂₅ = C₃₅ sen α₃₅.

Moltiplicando fra loro queste dieci equazioni si ha:

S₄₁ S₅₂ S₁₃ S₂₄ S₃₅ = S₄₂ S₅₃ S₁₄ S₂₅ S₃₁

formola che esprime appunto il teorema enunciato.

Ottavo teorema. Se in un poligono piano qualsivoglia si fissa un punto interno, dal quale si tirino rette a tutt’i vertici, e ciascuna di esse si prolunghi fino a segare due lati di eguale rango a partire dal vertice per cui passa quella retta; otterremo su ciascun lato quattro segmenti; fra tutti questi segmenti ha luogo una relazione analoga a quella del teorema precedente, colla sola differenza che a ciascun segmentoFig 9 impiegato in questo teorema bisogna sostituire il prodotto di due segmenti che incomincino da uno stesso vertice e terminino ai due punti di sezione di un medesimo lato.

La dimostrazione di questo teorema è analoga a quella del precedente.

Nono teorema (di Carnot). Se un fascio di rette in un piano (fig. 9.ª) OA, OA₁, OA₂, ... passanti per uno stesso punto O vien segato da due trasversali rettilinee nelle due serie di punti A, A₁, A₂, ...; a, a₁, a₂, ... le diagonali de’ quadrilateri AA₁a₁a, A₂A₃a₃a₂, ... s’intersecano nei punti m, m’, ... i quali sono situati in una retta passante pel punto comune alle due trasversali.

Ecco la dimostrazione statica data dal Coriolis di questo teorema, che è uno de’ più noti nella teorica delle trasversali.

Ai punti A, A₁, O applichiamo tre forze parallele, il cui centro sia m, ed ai punti A₂, A₃, O tre forze parallele ed opposte alle prime, aventi il loro centro in m’, e per modo che le due forze applicate in O si elidano fra loro. Per ciò non rimarranno che le quattro forze applicate in A, A₁, A₂, A₃ equivalenti a due forze applicate in m, m’; la loro risultante dovrà quindi passare pel punto comune alle rette AA₁, ed mm’. Ma alle prime forze applicate in A, O possiamo sostituire la loro risultante applicata in a, ed alle seconde forze applicate in A₂, O si può sostituire la loro risultante applicata in a₂; quindi ci rimarranno quattro forze applicate in A₁, A₃, a, a₂ il cui centro dovrà cadere sì nella A₁A₂ che nella aa₂; dunque è dimostrato il teorema.

---