 i contorni di
i contorni di  . Siano
. Siano  e
e  quei pezzi del contorno
quei pezzi del contorno  (fig. 45), i cui punti rispettivamente appartengono e non appartengono al contorno
(fig. 45), i cui punti rispettivamente appartengono e non appartengono al contorno 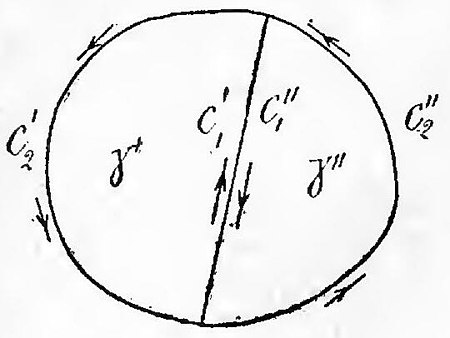 Fig. 45.
Fig. 45. e siano
e siano  e
e  quei pezzi di
quei pezzi di  i cui punti rispettivamente appartengono al controno
i cui punti rispettivamente appartengono al controno  .
.
Sarà:

 .
.
Evidentemente  e
e  sono archi di curve coincidenti, ma percorsi in verso opposto. Quindi:
sono archi di curve coincidenti, ma percorsi in verso opposto. Quindi:
 ,
,
e perciò dalle precedenti formole si ottiene, sommando:
 .
.
Ma  e
e  formano complessivamente il contorno
formano complessivamente il contorno  di
di  , e sono percorsi nello sesso verso, sia come appartenenti al contorno di
, e sono percorsi nello sesso verso, sia come appartenenti al contorno di  o
o  , sia come appartenenti al contorno di
, sia come appartenenti al contorno di  . L'ultima equazione dà dunque:
. L'ultima equazione dà dunque:
 .
.
Questo teorema si può enuncaire dicendo:
Lo integrale  esteso al contorno di un campo
esteso al contorno di un campo  è una funzione additiva di
è una funzione additiva di  .
.
Ciò rende intuitivo che in molti casi tale integrale curvilineo si potrà trasformare in un integrale superficiale esteso a  .
.
Ciò appunto è approvato dal seguente teorema, da cui risulta precisamente che la derivata di tale funzione additiva vale comunemente  .
.
 Fig. 45. e siano e quei pezzi di i cui punti rispettivamente appartengono al controno .
Fig. 45. e siano e quei pezzi di i cui punti rispettivamente appartengono al controno .























