| Questa pagina è stata trascritta e formattata, ma deve essere riletta. |
| LIBRO PRIMO. | 32 |
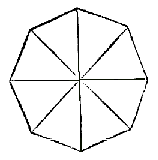
è de dentro della figura doue ciascun di loro terminano con uno angolo occupando tutto quello spacio che attorno al predetto ponto, ilquale spacio sempre sè equalia a quattro angoli retti, come in fine della terciadecima propositione fu detto, & approuato adonque de quelli sedeci angoli retti ne caueremo quattro per regola, cioè per li quattro fatti attorno al ponto, resta duodeci per il numero dalli angoli retti a chi se equaliano li otto angoli della datta figura, che è il proposito. Anchora el se manifesta per le cose ditte che protrahendo ciascun lato d’una figura moltiangolo tutti li angoli estrinsici gionti insieme se equaliano a quattro angoli retti che cosi se dimostrarà, sopra il penthagono .a.b.c.d.e. protratto il lato .a.b. fina in f. il lato .b.c. fin a .g. il lato .c.d. fin in .h. il lato .d.e. fin in .k. il lato .e.a. fin in .l. hor dico che tutto l’angolo .a. intrinsico del penthagono con l’angolo estrinsico sono equale a duoi angoli retti per la tertiadecima propositione, & per la medesima ragione li duoi angoli .b. intrinsico & .b. estrinsico, & cosi de tutti li altri, per laqual cosa li angoli .a.b.c.d.e. intrinsici & estrinsici seranno fra tutti equali a diece angoli retti, ma perche li cinque angoli del ditto penthagono son è quali a sei angoli retti, come di sopra fu demostrato. Adonque se delli detti diece angoli retti a chi se
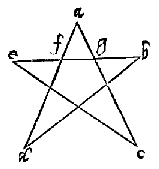
equaliano li predetti angoli intrinsici & estrinsici del penthagone cauaremo li sei, a chi se equalia li cinque angoli intrinsici, cioè quelli del penthagono resteranno quattro per li angoli estrinseci, cioè li angoli .b.a.l.c.b.f.d.c.g.e.d.h. & .a.e.k. adonque tutti li ditti angoli estrinseci del predetto penthagono si egualiano a quattro angoli retti, & cosi riuscirà in ciascun’altra figura poligonia che è il proposito.
Anchora è manifesto, che di ogni penthagono, delqual caduno lato sega dui delli altri lati, ha cinque angoli equali a duoi angoli retti.
Sia il penthagono che se prepone .a.b.c.d.e. et conciosia chel lato .a.c. seghi lo lato .b.e. in ponto .g. & lo lato .a.d. seghi il medesimo in ponto .f. et l’angolo .a.f.g. serà equale alli duoi angoli .b. & .d. conciosia che quello sia lo estrinseco a quelli, in lo triangolo .f.d.b. similmente l’angolo .f.g.a. sarà equale alli duoi angoli .c. & .e. conciosia che quello sia lo estrinsico a quelli in lo triangolo .g.c.e. ma li dui angoli .a.f.g. & .f.g.a. insieme con l’angolo .a. sono equali a duoi angoli retti. Adonque li quattro angoli b.d. & .c.e. insieme con l’angolo .a. sono equali a duoi angoli retti che è il proposito.
33|33 Se in la sommità de due linee equidistante, & di equal quantità, siano congionte due altre linee, quelle medesime seranno anchora equale, & equidistante.
