| Questa pagina è stata trascritta e formattata, ma deve essere riletta. |
| LIBRO PRIMO. | 31 |
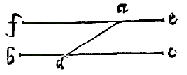
Sia il ponto .a. dato de fora della linea .b.c. dalquale bisogni tirare una linea equidistante alla linea .b.c. tirò la linea .a.d. cascante come si uoglia con la linea .b.c. constituendo l’angolo .a.d.c. & l’angolo .a.d.b. Et sopra el ponto .a. constituerò (per la dottrina della uigesima terza propositione) l’angolo .e.a.d. equale all’angolo .a.d.b. ouer l’angolo.f.a.d. equale all’angolo .a.d.c. (che darà quel medesimo) e perche li detti angoli sono coalterni, la linea .f.e. serà equidistante alla linea .b.c. (per la uigesima settima propositione) che è il proposito.
31|31 L’angolo estrinsico di ogni triangolo: d’un lato produto, è equale alli duoi intrinsici a lui oppositi, Et tutti li tre angoli intrinsici di quello è necessario esser equali a duoi angoli retti.

Sia el triangolo .a.b.c. e sia alongato el lato .b.c. fina in .d. dico che l’angolo a.c.d. estrinsico si è equale alli duoi angoli .a. & .b. intrinsici oppositi a se, insieme gionti; & che li tre angoli .a.b.c. del ditto triangolo .a.b.c. insieme gionti sono equali a duoi angoli retti e per dimostrar questo dal ponto .c. tirarò (per la dottrina della precedente) la linea .c.f. equidistante alla linea .a.b. & l’angolo .f.c.a. serà equale all’angolo ,a, (per la prima parte della uigesima nona) perche sono coalterni, & l’angolo .f.c.d. estrinsico serà equale all’angolo .b.intrinsico (per la seconda parte della medesima uigesima nona propositione) per laqual cosa tutto l’angolo .a.c.d. estrinsico si è equale alli duoi angoli.a. & .b. intrinsici a lui oppositi che el nostro primo proposito, & perche li duoi angoli .a.c.b. et .a.c.d. son equali a duoi angoli retti (per la terza decima propositione) adonque li tre angoli .a.b. et .c. intrinsici del triangolo seranno equali a dui angoli retti che è il secondo proposito, et nota che per questa propositione è manifesto che tutti li angoli de ogni figura moltiangola tolti insieme sono equali a tanti angoli retti quanto è el numero ch’ella è distante dalla prima, duplicato uerbigratia delle figure moltiangole, ouero poligonie la prima de tutte si è il triangolo, perche non si puo formar figura de rette linee de mancho de tre lati, perche con duoi linee rette non si puo constituire figura superficiale (per la ultima petitione) pero el triangolo è la prima figura de rette linee, la seconda figura si è il quadrilatero, la terza si è il penthagono, ouero figura de cinque lati & angoli & cosi ascendendo el numero delli lati ouero angoli a qual numero, si uoglia; cauando di quello el numero binario el rimanente serà el numero dell’ordine della figura come Esempli gratia de una figura de otto lati, & angoli per uoler el numero ordinario della detta figura caua de
