| Questa pagina è stata trascritta e formattata, ma deve essere riletta. |
| DI EVCLIDE |
è equal all’angolo .e.c.b. & questo è il secondo proposito, cioè, che li angoli, che sono sotto alla basa sono equali, & l’angolo .b.c.d. è equale all’angolo.e.b.c. Ma perche tutto l’angolo .a.b.e. è equale all’anggolo .a.c.d. (come di sopra fu approuato) adonque, per la terza concettione, l’angolo .a.b.c. (residuo) è equale all’angolo .a.c.b. (residuo) l’uno è l’altro di quelli è sopra la basa, che è il proposito.
6|6 Se dui angoli de alcun triangolo saranno equali, etiam, li dui lati risguardante quelli angoli, saranno equali.

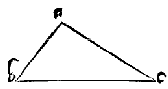
Questa è il conuerso della precedente inquanto alla prima parte di quella: perche essendo il triangolo .a. b. c. delquale li duoi angoli .b. & c. siano equali dico che il lato .a.b. è equale al lato .a.c. Perche se non sono equali, per l’aduersario, l’un di quelli necessita sia maggiore dell’altro, hor poniamo, che possibile fusse, che il lato .a.b. sia maggiore. Adonque dal lato .a.b. maggiore ne segaremo una parte alla equalità del minore, per la terza propositione, talmente che il superfluo sia dalla banda uerso .a. hor sia resecato in ponto .d. & sia la .b.d. equale alla .a.c. & sia protratta la linea .c.d. Intendo adonque li duoi triangoli .a.b.c. & d.b.c. liquali prouerò esser equilateri & equiangoli. Perche li duoi lati .d.b. & b.c. del triangolo .d.b.c. sono equali alli duoi lati .a.c. & b.c. del triangolo a.b.c. e l’angolo .b. è equale all’angolo .c. totale per il presupposito: adunque la basa .d.c. è equale alla basa .b.a. & l’angolo .d.c.b. è equale all’angolo .a.c.b. cioè la parte è equale al tutto, che è impossibile.
Nota che l’angolo .d.c.b. uerria a esser equale allo angolo .b. ma perche l’angolo ,a.c.b. è etiam lui equale al detto angolo .b. dal presupposito seguita per commune sententia l’angolo ,d.c.b. esser equale all’angolo .a.c.b. la parte al tutto che è impossibile.
7|7 Se dalli duoi ponti terminanti alcuna linea retta usciranno due linee rette, lequale concorrino a uno medesimo ponto è impossibile dalli medesimi ponti esser dutte altre linee equale alle sue conterminale che concorrino ad altro ponto da quella medesima parte.
