Metodo per rendere la Geometria indipendente dal principio della sovrapposizione
| Questo testo è completo. |
independente dal principio
della sovrapposizione
Del P. Giuseppe Maria Pagnini
P. Professore di Letteratura latina
Nell'università di Pisa
Membro Ordinario
Per me, secluso impositu, aequa trigona patescunt.
Troppo son io lontano dall'opinion di certuni, i quali stimano, che il celebre principio e comunemente adottato della sovrapposizione, che altri chiamano congruenza, poco o nulla sia degno della Geometria teorica, e però bramano che da questa sia onninamente sbandito. Per verità un tale principio non consiste, come sembra per avventura a costoro, in una grossolana e meccanica operazione, qual è quella d'un artefice, che più e più volte vada applicando la misura d'un piede a una parete per rintracciare in tal guisa con l'ajuto delle mani quanto sia lunga. La dimostrazione appoggiata alla sovrapposizione geometrica è una vera e genuina operazione d'intelletto, che meditando trasporta una figura sopra d'un'altra: e primieramente guidato dall'evidenza assume per cosa certa, che se alcune parti d'una figura sieno uguali ad alcune parti d'un altra; per esempio una linea retta ad una linea retta, ed un angolo ad un angolo, le dette parti sovrapposte le une alle altre si cuoprono e si combaciano esattamente. Poscia dal combaciarsi di queste parti si deduce per via di raziocinio il combaciarsi di tutte l'altre; dal che risulta la perfetta eguaglianza delle figure, in virtù di quell'assioma: le cose, che si combaciano insieme, sono uguali tra loro. Questo principio semplice, chiaro e dedotto dalla natura medesima delle cose, produce una vera e perfetta dimostrazione.
Quantunque però un tale principio meriti d'essere approvato e ricevuto nella Geometria, tuttavolta non sembra che debba essere biasimata l'industria di chi abbia scoperto qualche altro mezzo valevole a dimostrare quelle medesime verità, le quali mediante il prelodato principio si trovano già dimostrate. I tentativi, che da parecchi a tal effetto si sono fatti in addietro, non han potuto meritare la comune approvazione e il pubblico gradimento.
Alcuni anni sono fu da me pubblicato con le stampe un picciolo scritto, che ha per titolo: de principio superpositionis geometriae non necessario; d'onde apparisce che la geometria può essere independente da così fatto principio. Il mio metodo è stato da molti uomini intenditissimi esaminato, e per loro attestazione riconosciuto giusto e sicuro. Questo metodo stesso da me ridotto a maggior brevità, facilità e chiarezza ritorna in luce a qualche siasi giovamento o diletto di que', che amano una tal sorta di studj.
ASSIOMA (Fig. 2.)
Se due triangoli ABC, a b c sono equilateri ed equiangoli tra loro, cioè tali che tutti e tre i lati AB, BC, CA dell'uno sieno uguali a tutti e tre i lati a b, b c, c a, dell'altro, ciascuno a ciascuno, e tutti e tre gli angoli A, B, C sieno uguali a tutti e tre gli angoli a, b, c, compresi da lati uguali, essi triangoli sono totalmente uguali tra loro.
La cosa è manifesta: poichè in tale supposizione ambedue i triangoli hanno uguali tutti i loro costitutivi, che sono i tre lati e i tre angoli, e nula resta a potersi assegnare, onde sia l'uno di loro diverso e differente dall'altro. Perciò anche l'aree, o vogliam dire gli spazj occupati e compresi da loro, debbon essere uguali.

LEMMA
Se nel diametro AB d'un cerchio si prenda fuori del centro C un punto D, d'onde sieno tirate nel semicerchio alla circonferenza tre rette DE, DF, DG, la retta DE più vicina alla retta DCA, che passa pel centro, sarà maggiore della retta intermedia DF, e questa sarà maggiore della terza DG. (fig. 1.)
Dal centro C si tirino a punti E, F, G le rette CE, CF, CG. Perchè nel triangolo EHC le due rette EH, HC prese insieme sono maggiori della terza EC secondo l'assioma d'Archimede generalmente adottato1, saranno maggiori ancora della retta FC, per essere EC, FC uguali, siccome raggi del medesimo cerchio. Tolta via la retta comune HC, sarà la rimanente EH maggiore della rimanente FH. Presa poscia in comune la retta HD, sarà la EH insieme con la HD, cioè tutta la ED, maggiore delle due FH, HD. Ma queste nel triangolo FHD prese insieme sono maggiori della FD. Con lo stesso raziocinio si dimostra che la FD è maggiore della GD. Dunque la retta ED più vicina alla DCA, che passa pel centro, è maggiore della retta intermedia FD, e questa è maggiore della terza GD.
SCOLIO
La verità di questo Lemma si dimostra nella stessa maniera, se il punto D sia preso nelle estremità B del diametro AB.
PROPOSIZIONE I.
Dato un triangolo FCD, il quale abbia due lati FC, CD costanti in lunghezza, e il lato o base FD variabile, se l'angolo FCD divien maggiore o minore, anche la base FD diverrà maggiore o minore; e se la base FD divien maggiore o minore anche l'angolo FCD diverrà maggiore o minore.
Prima parte. Dal punto C con l'intervallo d'un lato FC, il quale sia non minore dell'altro lato CD, descrivasi la circonferenza FABF, e prolunghisi il lato CD quanto è necessario per compiere il diametro ACDB. Supposto immobile il lato CD, affinchè l'angolo FCD divenga maggiore o minore, è necessario che il lato FC movendosi intorno al punto C vada a terminare in qualche punto E dell'arco FA o in qualche punto G dell'arco FB. Onde nel primo caso la base variabile FD dee farsi uguale a ED, e nel secondo caso dee farsi uguale a GD. Ma la ED è maggiore, la GD è minore della FD (Lemma). Dunque se l'angolo FCD divien maggiore o minore, anche la base FD divien maggiore o minore.
Seconda parte. Premesse le stesse cose che nella prima, affinchè la base FD divenga maggiore o minore, è necessario che ella insieme col lato o raggio FC si muova intorno alla circonferenza AFD, e vada a terminare, come sopra, a un qualche punto E dell'arco FA, o ad un qualche punto G dell'arco FB. Ma nel primo caso l'angolo FCD diviene maggiore, qual è l'angolo ECD; nel secondo caso divien minore, qual è l'angolo GCD. Dunque se la base FD divien maggiore o minore, anche l'angolo FCD divien maggiore o minore.
COROLLARIO
Dati due triangoli ECD, GCD, i quali abbiano due lati EC, CD uguali a' due lati GC, CD,
- Se l'angolo ECD è maggiore dell'angolo GCD, anche la base ED sarà maggiore della base GD,
- Se la base ED è maggiore della base GD, anche l'angolo ECD sarà maggiore dell'angolo GCD.
PROPOSIZIONE II.
Se due triangoli ABC, abc sono equilateri tra loro, cosicchè i tre lati AB, BC, CA sieno uguali a' tre lati ab, bc, ca, ciascuno a ciascuno, essi triangoli sono totalmente uguali. (fig. 2.)
Dimostro in primo luogo che l'angolo A è uguale all'angolo a. Poichè i due lati AB, AC del triangolo ABC sono uguali ai due lati ab, ac del triangolo abc, se l'angolo A fosse maggiore o minore dell'angolo a, anche la base BC del primo sarebbe maggiore o minore della base bc del secondo (Corol. prop. I n. 1.). Ma la base BC è uguale per ipotesi alla base bc. Dunque anche l'angolo A è uguale all'angolo a. Nella stessa guisa dimostreremo che l'angolo B è uguale all'angolo b, e l'angolo C all'angolo c. Dunque i triangoli ABC abc che son tra loro equilateri, sono eziandio equiangoli tra loro. E perciò sono totalmente uguali. (Assioma).
PROPORZIONE III.
Se due triangoli ABC, abc hanno due lati AB, AC uguali a due lati ab, ac, e uguali gli angoli A, a compresi da' lati uguali, essi triangoli sono totalmente uguali.
Essendo uguali i due lati AB, AC a' due lati ab, ac, se la base BC fosse maggiore o minore della base bc, anche l'angolo A sarebbe maggiore o minore dell'angolo a (Corol. prop. I. n. 2.) Ma l'angolo A per ipotesi è uguale all'angolo a. Dunque anche la base BC è uguale alla base bc. Adunque tutti e tre i lati del triangolo ABC sono uguali a tutti e tre i lati del triangolo abc, ciascuno a ciascuno. Essendo pertanto i detti triangoli equilateri tra loro, sono totalmente uguali (Propos. II.)
SCOLIO
Tutto il resto della Geometria, a riserva di queste due nostre proposizioni 2 e 3, che corrispondono all'ottava ed alla quarta del primo libro d'Euclide, si trova ben dimostrato comunemente senza il principio della sovrapposizione. Perciò qualora venga accettato e messo in pratica il metodo sovraesposto, la Geometria resta libera e indipendente dal divisato principio2.
Note
- ↑ Chi amasse di veder dimostrato quoesto assioma a foggia di teorema, speriamo che possa essere soddisfatto della seguente dimostrazione.
Due lati d'un triangolo ABC pressi in qualunque modo AB, AC unitamente, sono maggiori del terzo BC. (fig. 3.).

Fig. 3.
Se ciascuno de' lati AB, AC non è minore del lato BC, è cosa evidente, che ambedue quelli insieme sono maggiori di questo. Sia pertanto ciascuno de' lati AB, AC minore del lato BC. Supponiamo che questi due lati si rivolgano intorno a' punti B, C al disotto della base BC, cosicchè ne risultino le rette HB, HC uguali alle AB, AC, ciascuna a ciascuna: dal punto B col raggio BA descrivasi il cerchio ADE, il quale taglierà il lato maggiore BC in un punto D, e passerà pel punto H. Parimente dal punto C col raggio CA descrivasi il cerchio AFG, il quale segherà il suddetto lato maggiore CB in un punto F, e passerà pel medesimo punto H; dunque i due cerchi ADE, AFG s'incontrano insieme in due punti A, H posti di sopra e di sotto della retta BC; perciò debbono di fra loro segarsi in modo, che l'arco ADH del primo cada verso la parte C, e l'arco AFH del secondo cada verso la parte B. Ciò stabilito, perchè la BA è uguale alla BD, e la BD è maggiore della BF, anche la BA sarà maggiore della BF. E perchè la AC è uguale alla CF, sarà la BA insieme con la AC maggiore della BF insieme con la FC, cioè di tutta la retta BC. Adunque ec.
Il celebre Signor Abate Venini ha dato le migliori definizioni, che desiderare si possano della linea retta e della linea curva, cioè: la prima è quella che rivolgendosi intorno a due de' suoi punti non chiude spazio; la seconda è quella che rivolgendosi intorno a due de' suoi punti racchiude spazio. Dal che si deduce aperissimamente, che se la retta e la curva hanno gli stessi termini, la prima è più breve della seconda. Con la stessa evidenza si conosce, che se un triangolo si rivolge intorno a un suo lato, questo lato, che nella sua rivoluzione non chiude spazio, è minore degli altri due lati, che rivolgendosi intorno al detto lato chiudono spazio. - ↑ Merita osservazione il modo facile ed elegante, che il nostro metodo somministra per dimostrare la proposizione quinta del libro I d'[[Autore:Euclide. La dimostrazione, che questi ne dà a tenor del suo metodo, quanto è sottile e ingegnosa, altrettanto riesce lunga e scabrosa ad essere ben intesa da' principianti. Ecco la nostra dimostrazione.
In un triangolo equicrure ABC gli angoli m n posti sopra la base BC sono uguali. (Fig. 4.)
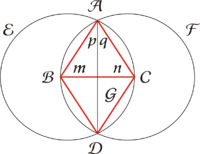
Fig. 4.
Dal punto B col raggio BC descrivasi il cerchio od arco CDE e dal punto C col medesimo raggio CB descrivasi il cerchio od arco BDF. Poscia dal punto D, nel quale si segano i due cerchi al di sotto del triangolo ABC, si tirino a' punti B, A, C le rette DB, DA, DC. Perchè nel cerchio CDE il raggio BD è uguale al raggio BC e nel cerchio BDF il raggio CD è uguale al medesimo raggio BC, sono le due rette BD, CD uguali tra loro: e perchè la AB si pone uguale alla AC, e la AD è comune ai due triangoli ABD, ACD, questi due triangoli sono equilateri tra loro, e perciò interamente uguali (prop. 2). Onde gli angoli o, p compresi dagli uguali lati sono uguali. Oltre a ciò perchè ne' triangoli ABG, ACG il lato AB è uguale al lato AC, il lato AG a entrambi è comune, e uguali sono gli angoli o, p compresi dagli uguali lati; i detti triangoli sono interamente uguali (prop. 3.) e perciò uguali son gli angoli m, n opposti al lato comune AG.
La costruzione della presente figura unita alla nostra dimostrazione è un fonte copioso di corollarj utilissimi, che a prima vista possono essere conosciuti da tutti quelli, che sono alquanto versati nella Geometria.

